Transform Your Grades, Transform Your Future

Expert Online Tutoring That Matches Your Curriculum, State Board, and One-on-One Support for K-12 Students

Explore articles on exam prep, time-management hacks, study resources, and global curriculum updates. .
Whether it’s O/A Levels, State Boards, or International exams, our blog keeps you ready and informed.

Book free trial Free worksheets

Get 60 Minute free trial class

Experience personalized tutoring. Book a one-hour free trial on your preferred subject and see how WebGrade Tutors can make learning fun, effective, and stress-free.

Understanding Probability: From Coin Flips to Real-World Chances

Why Probability Matters More Than Students Think

“Why do I need to learn this?”—If you’ve ever heard your child complain about probability homework, you’re not alone. Many students feel probability is just about flipping coins or rolling dice. Parents worry: Will my child struggle in exams if math feels this abstract?

Probability sounds like a fancy word. But really, it’s just about how likely something is to happen. Whether it’s flipping a coin, predicting weather, or deciding exam strategy, understanding probability gives students confidence—and helps parents support them more.

What is Probability

Probability is the branch of mathematics that deals with the occurrence of random events. Its value lies between 0 and 1, where 0 means impossibility and 1 means certainty.

The formula:

P(E)= number of favorable outcomes/total number of equally likely outcomes

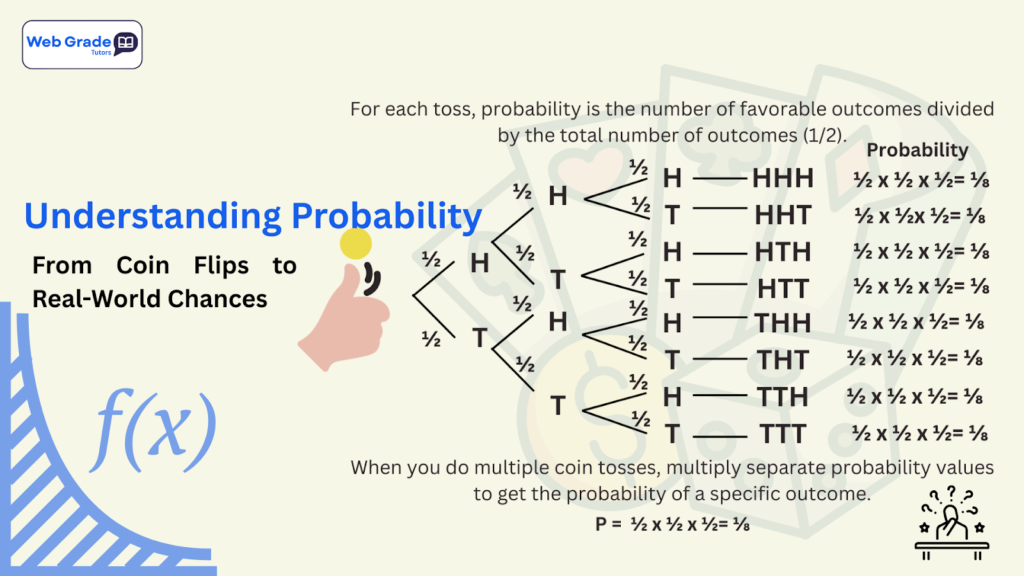
For example, flipping a fair coin: the probability of “Heads” = 1 favourable (Heads) ÷ 2 total (Heads or Tails) = ½

Probability helps us quantify uncertainty. It’s not about knowing for sure, but understanding how likely something is. That’s very useful in exams, but also when making decisions—what umbrella to take, whether to gamble, how to interpret forecasts.

Understanding Probability

Probability is simply the study of likelihood.

Coin flip: Two outcomes → Heads or Tails. Probability = 1 out of 2 (50%).
Dice roll: Six outcomes. Probability of rolling a 6 = 1 out of 6 (≈16.7%).
Everyday life: A weather forecast of 60% rain means rain happens on about 6 out of 10 similar days.

Probability = (Number of favorable outcomes) ÷ (Total possible outcomes).

Types of Events & Probability

Here are some important ideas to know:

A certain event

An event that always happens (probability = 1). E.g., the sun is rising tomorrow.

Impossible event

An event that can never happen (probability = 0). E.g., rolling a 7 on a standard six-sided dice.

Likely / Unlikely

Events in between. E.g., chance of rain, chance of drawing an Ace etc.

Complementary events

Two events that cover all possible outcomes. If A is “Heads”, its complement is “Tails”. P(A) + P(not A) = 1.

Rules of Probability

Some of the basic rules:

Probability Addition rule

(for events that don’t overlap)
If A and B are two events that can’t happen at the same time,
P(A or B)=P(A)+P(B)

 Example: Probability of rolling a “1” or a “2” on a dice = 1/6 + 1/6 = 2/6 = 1/3.

Probability Multiplication rule

(for independent events)
If two events are independent (the outcome of one doesn’t affect the other), then
P(A and B)=P(A)×P(B)

 Example: Flipping a coin twice: chance both are Heads = ½ × ½ = ¼.

Probability Complement rule

P(not A) = 1 − P(A).
If the chance it rains is 0.7, the chance it doesn’t rain is 0.3.

Real-Life Examples of Probability

The weather forecast says “80% chance of sunshine: That means in 8 of 10 similar days, it has been sunny. Helps decide whether to pack a hat, umbrella, etc

Drawing a card from a deck: Chance of drawing a red card = 26 red cards ÷ 52 total = ½

Rolling two dice: What is the chance both dice show 4? → (1/6) × (1/6) = 1/36.

Medical test accuracy: If a test is 95% accurate, probability helps understand false positives vs true positives.

Why Probability Matters for Exams & Everyday Life

Exam importance: Many school-tests and standardised exams include probability and statistics. If students understand it well, they often perform better in questions about data, risk, percentage, etc.
Decision making: From choosing travel insurance to understanding health risks, probability helps make safer and smarter choices.
Building logical thinking: Learning how to break down problems, use step-by-step reasoning, and avoid misinterpretations.

Probability exercises You Can Try at Home

Exercise 1 (10 minutes): Flip a fair coin 20 times. Count how many Heads, how many Tails. What fraction of flips were Heads? Compare with ½.
Exercise 2 (15 minutes): Roll a dice and flip a coin together. How many times in 30 tries do you get “Coin = Heads AND Dice = 6”? What was the probability? Compare your result with the theoretical result (1/2 × 1/6 = 1/12).
Exercise 3 (15 minutes): Use a deck of cards. Draw one card. What is the probability you get a King? What is the probability you get a red King? Then draw two cards without replacing: probability both are Kings.

These help students see how theory matches reality—and when actual results differ, that’s okay. It’s part of learning.

Strategies to Make Probability Easy

1. Start with Simple Experiments

Nothing beats hands-on practice. Try flipping coins, rolling dice, or drawing cards. Compare what actually happens (experimental probability) with what should happen (theoretical probability).

2. Use Stories and Games

Probability comes alive when tied to interests:

Predicting goals in a football match.
Guessing the next card in a game.
Checking daily weather and seeing if it matches the forecast.

3. Build Up Gradually

Start with one event (a single coin flip).
Then try two events (two coins, or coin + dice).
Finally, move to word problems that combine real-life situations.

Quick Exercises You Can Try at Home

Exercise 1: Coin & Dice Combo (15 minutes)

Flip a coin and roll a dice together.

Question: What’s the chance of getting Heads + a 6?
Answer: ½ × 1/6 = 1/12.

Try it 24 times and compare your child’s results with the theory.

Exercise 2: Weather Forecast Game (10 minutes)

Check tomorrow’s weather forecast.

Prediction: 40% chance of rain.
Ask your child: “Out of 10 days, how many should be rainy?”
Track results for the week. This makes probability real and fun.

Exercise 3: Card Deck Challenge (15 minutes)

Pick a card at random from a 52-card deck.

What’s the chance it’s red? (26/52 = ½).
What’s the chance it’s an Ace? (4/52 = 1/13).
Extra: Pick two cards without replacing. What’s the chance both are Aces? (4/52 × 3/51 = 1/221).

How Tutoring Helps You Master Probability

WebGrade Tutors know how to work, here’s how tutoring makes a difference.

Explains step by step: using simple words, real-life examples, and visuals.
Addresses where students get stuck: maybe the concept of “independent events” is fuzzy, or maybe mixing up “and/or.”
Practice with feedback: Immediate correction when there’s misunderstanding.
Builds confidence: Each solved example helps reduce anxiety about probability in exams.

Common Mistakes Students Make

It’s normal for students to get tripped up. Here are some classic mistakes:

Thinking past results change future ones

Example: After flipping 5 heads in a row, many students believe a tail is “due.” But each coin flip is independent. The chance of heads is always 50%, no matter what happened before.

Expecting perfect balance

Students think that in 10 flips, you must get 5 heads and 5 tails. In reality, you might get 7 heads and 3 tails. Over time, though, results average closer to 50/50.

Mixing up “zero probability” with impossible

Sometimes we say “almost zero chance,” but that doesn’t mean it can’t happen—it just means it’s very unlikely.

Understanding these pitfalls helps students feel more in control during exams.

Turning Confusion Into Confidence

Probability doesn’t have to be scary. With clear explanations, real-world examples, and a little practice, students can quickly move from “I don’t get it” to “This is easy!”

Ready to see the change? Book a free trial lesson with WebGrade Tutors today and watch your child’s confidence in math grow.

Ready to Boost Your Math Confidence?

Explore country-specific content, try a free 60-minute class, and join thousands of learners growing with WebGrade Tutors.

Visit our website

Explore content tailored to your curriculum and country—from foundational skills to exam prep.

Explore Content

Schedule a free 60-minute trial class

Connect with an expert tutor, experience our teaching style, and get a custom plan for success.

Book Free Trial

Join our community

Ask questions, get help, and grow your skills with students, parents, and tutors just like you.

Join Now

WebGrade Tutors — Learn smarter, not harder.

Our News & Blogs

Latests News & Blogs

view all blogs

Have Any Questions?

Have a inquiry or some feedback for us? Fill out the form
below to contact our team.

Our Address

85 Great Portland St London W1W 7LT, United Kingdom.

Phone Number

(+61) 480 008 636

Get in Touch

First Name

Last Name

Phone

Select Curriculum

Select Subject

Message

No Widget Added

Shopping cart